寻路算法——Jump Point Search

发表于   |  

很多游戏中需要实现自动寻路功能，在连续的地图坐标中搜索路径，需要分为两步，首先是离散化，再进行路径搜索。本文主要讨论路径搜索算法 Jump Point Search，以下简称 JPS。

在不考虑地图预处理的情况下，JPS 是基于格点的八方向寻路的最佳选择。为了理解 JPS，首先需要了解 A* 算法。

A* 搜索算法

A* 搜索算法，俗称A星算法，是很多寻路算法（包括JPS）的基础。该算法综合了 Best-First Search 和 Dijkstra 算法的优点：在进行启发式搜索提高算法效率的同时，可以保证找到一条最优路径。

Dijkstra 算法使用广度优先搜索解决赋权有向图的单源最短路径问题，可以找到两个顶点之间的最短路径。对于任一顶点 v，d[v] 表示从起点 s 到 v 的最短距离，显然 d[s] = 0，用 w[u, v]表示u到v的直达距离。该算法从原点s开始扩展，每一次针对顶点u，遍历其所有出边[u, v]，若d[v]>d[u]+w[u, v]，则将d[v]赋值为d[u]+w[u, v]。算法直至所有顶点都扩展过为止。下面的伪代码计算图G中原点s到每一顶点v的最短距离d[v]，并且保留v在此最短路径上的前趋顶点，以回溯出最短路径。算法维护两个顶点集合S和Q，集合S保留所有已知最小d[v]值的顶点v，集合Q则保留其他所有顶点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
function Dijkstra(G, w, s)
   for each vertex v in V[G]        // 初始化
         d[v] := infinity           // 将各点的已知最短距离先设成无穷大
         previous[v] := undefined   // 各点的已知最短路径上的前趋都未知
   d[s] := 0                        // 因为出发点到出发点间不需移动任何距离，所以可以直接将s到s的最小距离设为0
   S := empty set
   Q := set of all vertices
   while Q is not an empty set      // Dijkstra算法主体
         u := Extract_Min(Q)      // 将Q中有最小d[u]值的顶点u从Q中删除并返回u
          S.append(u)
          for each edge outgoing from u as (u,v)
                 if d[v] > d[u] + w(u,v)             // 拓展边（u,v）。w(u,v)为从u到v的路径长度。
                       d[v] := d[u] + w(u,v)         // 更新路径长度到更小的那个和值。
                       previous[v] := u              // 记录前趋顶点

如果只需在s和t之间查找一条最短路径的话，可以在第9行添加条件，如果满足u=t，则终止程序。下面的伪代码通过回溯，找出s到t的最短路径。

1
2
3
4
5
s := empty sequence 
u := t
while defined u                                        
      insert u to the beginning of S
      u := previous[u]      //previous数组即为上文中的p

可以看出，Dijkstra 算法在搜索时并不考虑终点的位置，而是盲目的搜索，因此效率并不高。贪婪最佳优先搜索解决了该痛点：在Dijkstra算法中，优先队列（即上面的Q）采用的是每个顶点到起点的距离排序，而贪婪最佳优先搜索中采用每个顶点到目标顶点的距离（一般可以用曼哈顿距离描述）进行排序。这里运用启发式思想，从搜索开始就向目标点方向优先搜索，在障碍物较少的情况下速度足够快，但路径不是最优。

如果用g(n)表示从起点到任意顶点n的实际距离，h(n)表示任意顶点n到目标顶点的估算距离，那么g(n)和h(n)就是Dijkstra算法与贪婪最佳优先搜索算法在顶点排序时分别使用的评估函数。而A*算法使用的评估函数为：

f(n) = g(n) + h(n)

这个公式具有以下特性：

  • 如果g(n)为0，即只计算任意顶点n到目标的评估函数h(n)，而不计算起点到顶点n的距离，则算法转化为贪婪最佳优先搜索算法；
  • 如果h(n)不高于实际到目标顶点的距离，则一定可以求出最优解，而且h(n)越小，需要计算的节点越多，算法效率越低，常见的评估函数有——欧几里得距离、曼哈顿距离、切比雪夫距离；
  • 如果h(n)为0，即只需计算起点到任意顶点n的最短距离g(n)，则转化为Dijkstra算法。

优化 A*

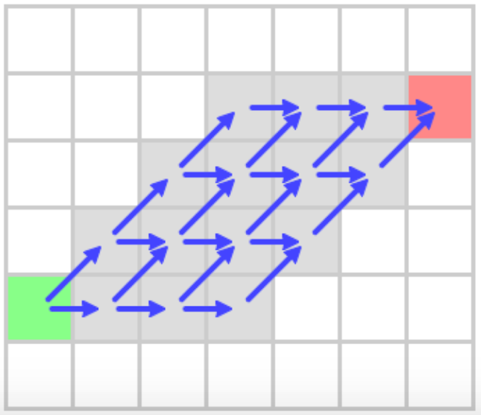
在两点之间的最短路径中，可能存在多条走法不同但长度相同的路径，这样的路径被称为是“对称”（symmetry）的，如下图所示。盲目搜索这类对称路径将严重影响搜索效率，而A*无法识别对称路径。作为目前最常用的寻路算法之一——JPS能够有效识别对称路径，并跳过它们。在40*40大小的格点地图上，A*算法找到一条最短路径大约需要180.05ns，而JPS只需15.04ns[1]。

对称路径

在基于格点的八方向寻路地图中，用$\vec{d}$表示八个方向之一（上、下、左、右等）。当从x开始沿着$\vec{d}$移动k个单元可以到达y时，可以表示为$y=x+k\vec{d}$。当$\vec{d}$为对角线移动时，将与$\vec{d}$ 45度的两个直线移动表示为$\vec{d_1}$和$\vec{d_2}$。路径$\pi=<n_1,n_2,…,n_k>$表示从$n_1$到$n_k$的无环顺序移动，$\pi$\x表示节点x不在路径中。len函数和dist函数分别表示路径的长度与两个节点之间的距离，如$len(\pi)$或$dist(n_0,n_k)$。

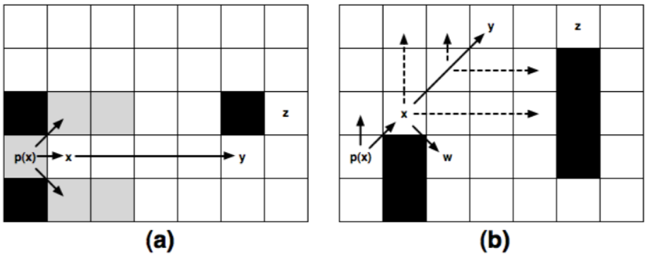
跳跃点示例

如上图所示，节点x的父节点为p(x)，当扩展x时，去考虑灰色的节点是没有意义的，因为从p(x)到达这些节点的路径在不包含x时更短，称这些灰色节点是劣性的。这时只有x右侧的邻居需要评估，但与A*算法直接将它加入开放列表不同，由于y拥有至少一个非劣节点（z），JPS算法会继续向右推进直到y。当找到一个y这样的节点（跳跃点），将它作为x的后继者，并赋于它g值，g(y)=g(x)+dist(x,y)。如果在前进过程中遇到障碍物，则当前方向的搜索失败。由此可见，JPS主要有两个优化策略：裁剪与跳跃。

针对节点x的邻居，裁剪的目的是识别其中的劣性节点，可以通过比较两条路径的长度来判断是否需要裁剪：从p(x)开始访问x到n结束的路径$\pi$，和从p(x)不经过x到n结束的路径$\pi’$。此外，$\pi$和$\pi’$中的节点都属于neighbours(x)。从p(x)到x是直线移动和对角线移动的两种情况需要不同的处理，如果x是起点，则不进行裁剪。

  1. 直线移动：对满足以下条件的任意结点$n\in neighbour(x)$进行裁剪，如下图(a)所示，需要裁剪除了n=5之外其他x的邻居。

len(<p(x),…,n>\x) <= len(<p(x),x,n>)

  1. 对角线移动：与直线移动唯一的区别在于这里需要严格的不等关系，如下图(c)所示，需要裁剪除了n=2、n=3与n=5之外的邻居。

len(<p(x),…n>\x) < len(<p(x),x,n>)

裁剪示例

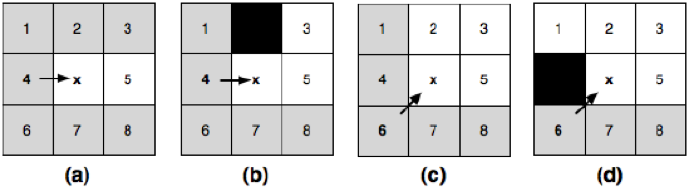
如果neighbours(x)不包含障碍，裁剪过后的结点被成为x的自然邻居（natural neighbours），如上图(a)和上图(c)中的非灰结点。当neighbours(s)包含障碍时，非自然邻居可能不都能被裁剪，这时，需要强制（forced）评估这类节点。

定义1 满足以下情况，则称节点$n\in neighbour(x)$是强制的：

  1. n不是x的自然邻居
  2. len(<p(x),x,n>) < len(<p(x),…,n>\x)

如上图(b)，直线移动的例子中n=3是强制的。而上图(d)中，n=1是强制的。

定义2 对于$y=x+k\vec{d}$，如果使得k最小，并且满足以下条件之一，则称节点y是从x出发，沿着方向$\vec{d}$的跳跃点。

  1. y是终点
  2. 根据定义1，y有至少一个强迫评估的邻居
  3. $\vec{d}$是对角线移动并且存在一个节点$z=y+k_i\vec{d_i}$（其中$k_i\in N$、$ \vec{d_i}\in {\vec{d_1},\vec{d_2}} $），使得在条件1和条件2下z是y的跳跃点。

上上图(b)中是条件3定义的跳跃点的例子，从x出发对角线移动至y，从y开始进行2次水平移动可以到达z，因此z是y的后继跳跃点，继而y是x的后继跳跃点。

计算单个节点的后继者的算法伪代码如下。首先，对当前节点x的邻居进行裁剪，接着对每个邻居n沿着x到n的方向尝试跳跃，将获得的跳跃点加入x的后继者中。

Require: x: current node, s: start, g: goal
successor(x)$\leftarrow\emptyset$
neighbours(x)$\leftarrow$ prune(x,neighbours(x))
for all n $\in$ neighbours(x) do
n $\leftarrow$ jump(x,direction(x,n),s,g)
….add n to successors(x)
return successors(x)

其中跳跃的算法伪代码如下。算法将初始节点沿着既定的方向移动，并检查移动后的节点是否满足定义2。满足时返回该节点（第5、7、11行），否则继续前进（第12行）。当遇到障碍或无法前进时递归结束（第3行）。

Require: x: initial node, $\vec{d}$: direction, s: start, g: goal
$n\leftarrow step(x,\vec{d})$
if n is an obstacle or is outside the grid then
….return null
if n = g then
….return n
if $\exists n’\in neighbours(n) s.t. n’$ is forced then
….return n
if $\vec{d}$ is diagonal then
….for all i $\in$ {1,2} do
……..if jump(n,$\vec{d_i}$,s,g) is not null then
…………return null
return jump(n,$\vec{d}$,s,g)

最后附上一个可以动态演示 JPS 寻路过程的网站。

参考文献

[1] S. Rabin, Game AI Pro 2: Collected Wisdom of Game AI Professionals, A K Peters/CRC Press, 2015.
[2] D. Harabor and A. Grastien, Online Graph Pruning for Pathfinding On Grid Maps, AAAI Conference on Artificial Intelligence, AAAI 2011, San Francisco, California, Usa, August DBLP, 2011.
[3] A search algorithm, https://en.wikipedia.org/wiki/A_search_algorithm.
[4] Amit, Pathfinding, http://theory.stanford.edu/~amitp/GameProgramming/.
[5] Dijkstra’s algorithm, https://en.wikipedia.org/wiki/Dijkstra%27s_algorithm.
[6] 游资网, 如何快速找到最优路线？深入理解游戏中寻路算法, http://www.gameres.com/777251.html, 2017.
[7] 萤火之森, 寻路算法-贪婪最佳优先算法, http://frankorz.com/2017/12/16/greedy-best-find-search/, 2017.