去年去网易面试,一个问题的大意是:一个三角形三个顶点分别是红、绿、蓝,即RGB值分别为(1,0,0)、(0,1,0)、(0,0,1)(或255表示,whatever),如何用RGB值表示三角形内任意一个点,即作线性插值。当时没有学过相关内容,临时想到用面积法做。最近才知道重心坐标(Barycentric Coordinates)的概念,可以方便的解决这个问题。
用重心坐标解决问题
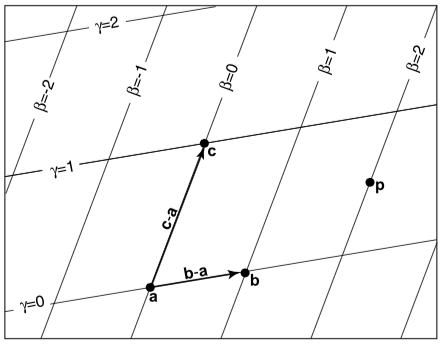
图 1
可以把重心坐标看作非直角坐标系,如图1所示。三角形的顶点分别为a、b、c,将 a 看作坐标系原点,a 到 b 和 c 的向量分别是基向量。那么任意点 p 可以表示成:
$$
p = a+\beta(b-a)+\gamma(c-a)
$$
移项得到:
$$
p = (1-\beta-\gamma)a+\beta{b}+\gamma{c}
$$
定义一个新变量$\alpha$,使得:
$$
\alpha \equiv 1-\beta-\gamma
$$
得出:
$$
p(\alpha,\beta,\gamma) = \alpha{a}+\beta{b}+\gamma{c}, 其中 \alpha+\beta+\gamma = 1
$$
所以,点p的重心坐标就是$(\alpha,\beta,\gamma)$。
重心坐标不仅可以表示三角形abc内的点,也可以表示平面内的任意点。任意点p在三角形abc内部,当且仅当
$$
0<\alpha<1,
0<\beta<1,
0<\gamma<1,
$$
当一个坐标为0,其余两个在(0,1)区间时,点落在三角边上;如果两个坐标为0,另一个为1时,点落在三角顶点上。
这时,回到面试题上,任一点p的RGB值可以表示为$(255 \times \alpha, 255 \times \beta, 255 \times \gamma)$。
求解重心坐标
可以看出,重心坐标是齐次坐标的一种。如果给定点p,如何计算它的重心坐标呢。
定义法
最直接方法是将点代入定义,解出$\beta,\gamma$。还有两种根据重心坐标的特性的解决方法。
几何法
重心坐标的一个几何特性是,坐标值是点到三角边距离的缩放有符号表示(scaled signed distance)。如下图。
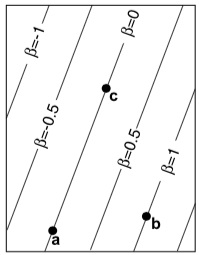
图 2
比如,对于直线 f(x,y)=0,f(x,y)表示点到该直线的缩放有符号距离。如果f(x,y)=0表示一条直线,那么kf(x,y)=0也一样。改变k可以控制点到该直线的距离和直线两边的符号。我们选择k,使得$kf(x,y)=\beta$,其中,在b点处$\beta=1$,以此确定k。因此,如果$f_{ac}(x,y)=0$经过a、c点,可以计算某一点(x,y)的$\beta$值:
$$
\beta = \frac{f_{ac}(x,y)}{f_{ac}(x_b,y_b)}
$$
面积法
连接三角形重心与定点,将三角形分为三份,如下图。重心坐标为
$$
\alpha = A_a/A,
\beta = A_b/A,
\gamma = A_c/A,
$$
其中,$A = A_a+A_b+A_c$,
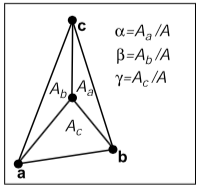
图 3
当时面试时答的用这种方法确定系数,但并不知道重心坐标的概念。。
参考资料
[1] Mathematics for 3D Game Programming and Computer Graphics, 3rd Edition https://book.douban.com/subject/6675562/
[2] https://zh.wikipedia.org/wiki/%E9%87%8D%E5%BF%83%E5%9D%90%E6%A0%87